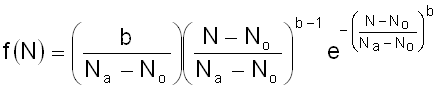Take a Test    Article Library    CEEJ Home    Submit an Article     Contact CEEJ

Article # 0025

ESTIMATION OF RESPONSE TIMES

USING A THREE FUNCTION WEIBULL DISTRIBUTION

Part 3

Dr. P. F. Packman (1) and Dr. J. L. Packman (2) 

(1)     Professor Emeritus, Dept. of Mechanical Engineering Southern Methodist University,  Dallas TX 75240

(2)     Assistant Professor, Dept. of Counseling and Educational Psychology, University of Nevada, Reno, NV, 89557

 

Weibull Function for the Analysis of the

Distribution of Response Times

 Gaussian or Normal Distribution

 

From the discussion presented above, it is reasonable to state that the use of a single value for reaction time is an oversimplification of the reaction time process for a large population.  Because of the large number of variables that enter into the reaction time of an individual it is important to consider the statistical variability of reaction times among a diverse population.  Rather than use a single value for all individuals, the engineer is more likely to use a cumulative distribution function.  This allows the single value for reaction time to be replaced with a probability statement.  A typical statement would then be in the form “75% of the population would have a reaction time of 1.8 seconds or less.”

 

The Gaussian or normal distribution is one of the most common statistical distribution functions used to describe the behavior of a population.  Many engineering properties are described using this function such as strength behavior, thermal behavior and fluid flow. Many psychological or medical experiments using limited number of human subjects are also described in terms of a normal or Gaussian distribution. The Gaussian distribution is an adequate description of the central tendency behavior.  This can be considered as bounded by the 80th percentiles. For the symmetrical Gaussian distribution 80% of the results will fall between these values.  There will be 10% of the data above and 10% of the data below these values.  Many experimental statistical studies of engineering properties can extend these percentiles to the 90th or 95th percentiles providing the sample size is large.  Most engineers use the Gaussian distribution because of the ease of analysis.  However it should be realized that while the Gaussian distribution adequately describes the statistics associated with behavior about the central mean, estimations in the low or high probability regions may be in error.

 

There are many properties and behaviors that are poorly described by the Gaussian function, particularly at the tails of the distribution. For this reason a number of other distribution functions have been developed.

 

Weibull Distribution

 

The Weibull distribution is a more powerful statistical distribution used to describe more complex behaviors than those described using the Gaussian distribution. The Weibull distribution is one of the most widely used distributions for life testing and can estimate very low probabilities of failure of components. . This distribution was initially developed by the Swedish engineer Waloddi Weibull (1951) initially as a characterization for the breaking strength of brittle materials.  The Weibull distribution function is given by

 

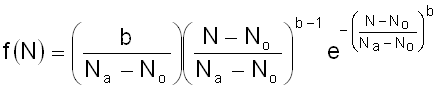                                                      Egu. 3

 

The cumulative Weibull distribution describes the probability of a failure prior to a life N given by

 

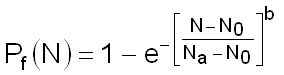                                                                                       Equ. 4

 

Where:

 b is the shaping parameter.

The value of No > 0 is the location parameter or the minimum life.

The value of Na is the characteristic life that locates the strength distribution i.e. life at 63.2% probability of failure.

 

A number of references discuss the Weibull distributions and their applicability. A good reference is Abernathy et al (1983).

 

The analysis of response time for a population appears to be a behavior that is ideally suited to a statistical description using a three function Weibull distribution.  The cumulative Weibull distribution function for the fraction of people whose response time is equal to or less than a given time T is given by;

 

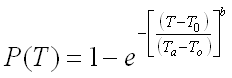                                                                                                          Equ.5

 

In this analysis:

To is the cut-off time, the minimum time that any person could respond

            Ta is the characteristic tendency for the distribution

            T is the independent variable time

            b is the shaping parameter

 

The cut-off time, To, is the time below which there can be no probability of responding.  It would be physically impossible for any subject to respond to the stimulus in a shorter time based on the physics of the human response.  Hence the probability of a response should be zero below this value. This is known as the Weibull location parameter.  

 

A Gaussian distribution is a two parameter distribution. These are the mean and standard deviation.  In a Gaussian distribution there is no location parameter and hence lower bound.  There is a small but finite probability of response even for extremely short times.  This behavior does not represent actual behavior and is a significant reason why the Gaussian distribution would be improper to use for a study of response times. 

 

The characteristic tendency, To, represents the response time for which the cumulative probability is 63.2%.  This means that at thus time at least 63% of the population has responded.  In a Gaussian distribution this would correlate to the central tendency or mean for which 50% of the population has responded. 

 

The strength of the Weibull distribution analysis lies in the shape factor, b.  This factor allows variations in the form of the distribution. The shape factor, b, determines the type of Weibull distribution to which the data belongs.  These are can be used to describe engineering types of failure modes, but analogous situations arise in other engineering and non-engineering situations. The shape factor may be of one of three general types

 

(1)   Where b <1.  This is describes a process for which there is a probability of early life failures.  Miss-assembly, early burnout failures and manufacturing difficulties fall in this category.  With b = 0.5 the distribution can describe a bath tub curve for which there are some early failures, followed by a period of no failures ending with an increase in failures as the product wears out.

 

(2)   Where b = 1.  This describes a process of random failures, usually independent of time. These have often been failures due to maintenance errors, electron random failures, and failures due to a multiplicity of problems.

 

(3)   Where b >1.  This describes failures due to wear-out failures, low cycle fatigue, fatigue, (b = 3) When b >>1 the process is a long time wear-out failure such as bearing failure, creep and corrosion failures.  A b = 3.57 approximates a Gaussian distribution.

 

In developing a Weibull three function distribution to describe the human response time behavior the following must be considered.

 

(1)   There is a time period below which no individual can be expected to respond because of human physical considerations. In this analysis that time has been selected as To = 0.95 seconds.
 

(2)   The characteristic life should be selected so that the average value of response time (50% probability of response) used by most engineers is met.  In this analysis that corresponds to Ta characteristic life that would produce a 50% response at 1.5 seconds.

 

(3)   A significant fraction of the population should have responded by a time of about 2.5 seconds to match the civil engineering highway safe viewing response distance.  This is chosen as having 90% of the population responding before 2.5 seconds.  

These requirements are met in a three function Weibull distribution with the following characteristics.

1. To = 0.95 seconds

2. Ta = 1.15 seconds

3. b = 1.15

 

Using the above constants, a three function Weibull distribution that can be used to describe human response time is given as

 

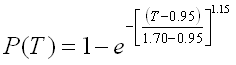                                                                                             Equ. 6

 

This equation satisfies the three first three criterion described above. Using this distribution function, Table II provides interpolation date giving the percentage of the population that would respond in a given time T.   Figure 1 plots the cumulative probability of responding as a function of time in seconds. For this three function Weibull analysis To = 0.95 sec., Ta = 1.15 sec., and b = 1.15. 

 TABLE II

 CUMULATIVE PERCENTAGE OF POPULATION

WITH A RESPONSE TIME T IN SECONDS

TO MATCH  90% RESPONSE IN 2.5 SEC.

No = 0.95 sec., Na= 1.70, sec., b= 1.15

TIME (sec)

RESPONSE  %

TIME (SEC)

RESPONSE %

0-,95

0

2.5

90.0

1

4.3

2.6

91.5

1.1

14.5

2.7

92.9

1.2

24.6

2.8

94.0

1.3

34.0

2.9

95.0

1.4

42.6

3.0

95.8

1.5

50.3

3.1

96.5

1.6

57.1

3.2

97.0

1.7

63.2

3.3

97.5

1.8

68.4

3.4

97.9

1.9

73.0

3.5

98.3

2.0

77.0

3.6

98.6

2.1

80.5

3.7

98.8

2,2

83.5

3.8

99.0

2.3

85.9

3.9

99.2

2.4

88.1

4.0

99.3

 

These Weibull analysis constants force the distribution to match with both the average estimate of 1.5 seconds, and yet match the highway safety requirement for 90% of the population being able to respond within 2.5 seconds.  The cumulative function estimates the fraction of the population that would be included in the tail of the distribution.  The cumulative percentage function when extended to a reaction time of 4 seconds, estimates that 99.3% of the population has response times equal to or less than 4 seconds.   This inference could not normally be estimated using a standard Gaussian distribution.   The Gaussian distribution because of the symmetry about the mean would also estimate similar percentages of the population had response times less than 0.95 seconds, which is impossible..  

 

The percentages of the populations with reaction times greater than 2.5 seconds might be applicable for a very large population that includes elderly and slower responding individual. This estimates that 10% of the population has reaction times greater than 2.5 seconds, 5% of the population has reaction times greater than 3.0 seconds, and 2% of the population has reaction times greater than 3.5 seconds. The desire to include elderly and possibly disabled populations may be the rationale for the highway line-of-sight requirements of 90% response at 2.5 seconds. 

  

Figure 1. Graph of the Cumulative Probability of Responding (fraction of responses) at or before a given time T estimated using a three function Weibull analysis. To = 0.95 sec. Ta = 1.7 sec.  b = 1.15.  To match 50% response at 1.5 sec., and 90% response at 2.5 sec.

 

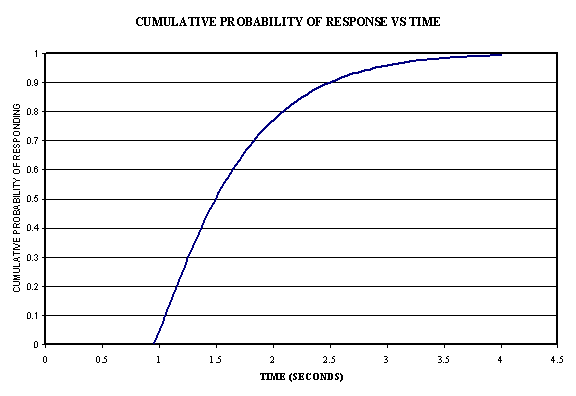
If the requirement were changed to require that 95% of the population responds within 2.5 seconds the tail of the distribution is modifies as shown in Table III.   Here the lower bound cut-off is retained at 0.95 seconds, and the average estimate is retained at 1.5 seconds.  What has changes is a decrease in the portion of the population having response times greater than 2.5 seconds.  The percentages of the population with response time greater than 2.5 seconds have been reduced from 10% to 5%.  At 3.0 seconds only1.2% of the population has not responded, at5 3.5 seconds 0.3% of the population has not responded. This stricter requirement might be applicable to a more limited population, for example younger drivers. 

 

TABLE III

 CUMULATIVE PERCENTAGE OF POPULATION

WITH A RESPONSE TIME T IN SECONDS

TO MATCH 95% RESPONSE AT 2.5 SEC.

No = 0.95 sec. Na = 1.66 sec., b = 1.42

TIME (sec)

RESPONSE  %

TIME (SEC)

RESPONSE %

0-,95

0

2.5

95.1

1

2.2

2.6

96.3

1.1

10.4

2.7

97.2

1.2

20.3

2.8

97.9

1.3

30.6

2.9

98.4

1.4

40.7

3.0

98.8

1.5

50.1

3.1

99.1

1.6

58.6

3.2

99.4

1.7

66.0

3.3

99.5

1.8

72.5

3.4

99.6

1.9

77.9

3.5

99.7

2.0

82.5

3.6

99.84

2.1

86.2

3.7

99.89

2,2

89.2

3.8

99.92

2.3

91.7

3.9

99.94

2.4

93.6

4.0

99.96

 Figure 2. Graph of the Cumulative Probability of Responding (fraction of responses) at or before a given time T estimated using a three function Weibull analysis. To = 0.95 sec. Ta = 1.66 sec.  b = 1.42.  To match 50% response at 1.5 sec., and 95% response at 2.5 sec.

 

 

Conclusions

 

While a large amount of research on reaction time appears in the literature, it is doubtful that a better quantitative evaluation of reaction time variations in real-life situations will be available in the immediate future. Work likely to produce practical results is expensive and difficult to conduct.  The number of variations on real life stressful conditions is large and the population subjected to these real-life conditions is becoming more diverse (c.f. Olson & Farber, 2005)  The use of a single response time of 1.5 seconds for all analysis while widely used appears oversimplified .  A deterministic analysis should be supplemented with a statistical analysis.  At present there are no tables or equations that can be used to estimate a specific response time for a given situation from the basic data. 

 

Most reaction time studies are very limited in scope and use test results from a small experimental population.  With a reduced number of subjects, the form of the statistical distribution for the experimental analysis is unclear, and a Gaussian distribution is often erroneously assumed.  In this analysis, a more realistic Weibull three function distribution is assumed and the cumulative distribution function estimated from limited data. 

 

References 

Abernathy, R. B., Breneman, J.E., Medlin,C. H., Reinman,G.L., (1983)  Weibull Analysis Handbook AFWAL TR 83-2079  AD AL143 100.,Nov.

 Anonymous, Clemson University, (2001) biointro.clemson.edu/bcp/bp/Lab/110/reaction.html

 Anonymous, Mother Nature, (2006) http://www.mothernature,com/Library/ Bookshelf/Books/44/51.cfm

 Anonymous, (2006) http://www.webs1.uidaho.edu/niatt labmanual/Chapters/geometricdesign/theory andconcepts.html.

 Anonymous, (2006) New York Times Science Section 31 January, p. 6. Reporting Study by Shipley, B. A., Psychosomatic Medicine, Univ. Edinburgh.

 Brebner, J. T., and Wellford, A. T., (1980)  Introduction, in Welford, A. T., (ed.) Reaction Times, Academic Press NY., pp.1-23.

 Deary, I. and Der, G.,(2005) Reaction Time and IQ May Predict Long Life, Medical Research News, 3 Feb. also Reaction Time Explains IQ’s Association with Death, Jan 2005, Psychological Science.

 Donders, F.C. (1868) On the Speed of Mental Processes Acta Psychologica,Vol. 30, pp 412-431. Translated by Koster, (1969

 Fankhauser, D.B. (2004) Visual Reaction Time, University of Cincinnati, Clermont College, OH,

 Fieandt, K., Huhtala, A., Kullberg, P., and Saarl, K., (1956) Personal Tempo and Phenomenal Time at Different Age Levels, Psychological Institute Reports, No. 2., University of Helsinki, Finland

 Froeberg, S. (1907)  The Relation Between the Magnitude of Stimulus and the Time of Reaction, Arch. Of Psychology, No 8.

 Galton, F., (1899) On Instruments for (1) Testing Perception of Difference of Tint and for (2) Determining Reaction Time, Journal of the Anthropological Institute, Vol. 19, pp 27-29.

Jensen, C., Schultz, G., and Bangerter, B., (1983) Applied Kinesiology and Biomechanics, McGraw Hill, NY. 

Keele, S., (1986) Motor Control, in Boff, K., Kaufman, L., and Thomas, J., (eds) Handbook of Perception and Human Performance, vol. 2, Cognitive Processes and Performance, Wiley, NY. 

Kohlfeld, D. L., (1971)  Simple Reaction Time as a Function of Stimulus Intensity in Decibels of Light and Sound, J. Experimental Psychology, Vol. 88., pp. 251-257.  

Lord, S. R and Fitzpatrick, R. C. (2001) Choice Stepping Reaction Time; A Composite Measure of Falls Risk in Older People, The Journal of Gerontology, Series A: Biological Sciences and Medical Sciences, Vol. 56, M627-M632. 

Morgan, C.T., et al (1963 and other editions) Human Factors Engineering Guide to Equipment Design, McGraw Hill Book Co. NY.,

Olson, P.L. and Farber, E., (2005) Forensic Aspects of Driver and Perception and Response, Second Edition, Lawyers & Judges Publishing Co., Inc. 

Sanders, M. S. and McCormick, E. J., (1993)  Humanf Factors in engineering and Design, Seventh Ed.,McGraw Hill Book Co, NY NY. 

Spencer, P.,(2000) Driving to Distractions, Womans Day, Sept 12, pp. 105-108. 

Staplin,L., Lococo, K. H., McKnight, A. J., McKnight, A. S., Odenheimer, G. L., (1998) Intersection Negotiation Problems of Older Drivers, Vol II, DOT HS 808850, Office of Research and Traffic Records, Nat. Highway Traffic Safety Admin., Washington DC. 

Weibull, W., (1951) A Statistical Distribution Function of Wide Applicability, J. App. Mech., Vol. 51, Sept., pp. 293-297. 

Woodson, W. E., Ed., (2005 and earlier editions) Human Factors Design Handbook,  MeGraw Hill book Company, NY NY. 

Welford, A. T., (1980) Choice Reaction Times, in Welford, A. T., (ed.) Reaction Times, Academic Press NY., pp.73-128. 

Wells, G. R., (1913) The Influence of Stimulus Duration on Reaction Time, Psychological Monographs, Vol. 15, 1066.

Article # 0025        TEST QUESTIONS:

 

1.   For the symmetrical Gaussian distribution ___ of the results will fall between these values. 

  1. 70%

  2. 75%

  3. 80%

  4. 90%.

2.   For the symmetrical Gaussian distribution, 10% of the data will outside these values.

  1. 20%

  2. 30%

  3. 40%

  4. 80%

3.   The two parameters of a Gaussian distribution are ____ .

  1. the cut-off time and the mean

  2. the mean and the standard deviation

  3. the cut-off time and the shaping parameter

  4. none of the above

4.   One advantage of the Gaussian distribution is ___.

  1. it includes a location parameter

  2. its accuracy at the high or low probability regions

  3. the ease of analysis

  4. none of the above

5.    A strength of the Weibull distribution analysis lies in the _____. 

  1. variability factor

  2. shape factor

  3. acceptable deviation factor

  4. none of the above

6.    A shape factor of b < 1 describes a process for which there is a probability of _____. 

  1. early life failures

  2. wear-out failures

  3. random failures

  4. none of the above

7.   A shape factor of b = 1 describes a process for which there is a probability of _____. 

  1. early life failures

  2. wear-out failures

  3. random failures

  4. none of the above

8.  A shape factor of b > 1 describes a process for which there is a probability of _____. 

  1. early life failures

  2. wear-out failures

  3. random failures

  4. none of the above

9.   The characteristic tendency or characteristic life represents the value for which the cumulative probability is ____.

  1. 36.8%

  2. 50%

  3. 55.5%

  4. 63.2%

10.  The Weibull distribution was initially developed  as a characterization for the ____ of brittle materials.

  1. breaking strength

  2. vibration resistance

  3. density

  4. glass factor

 

 

Take a Test    Article Library    CEEJ Home    Submit an Article     Contact CEEJ